Squence & Number Pattern

Squence & Number Pattern

In Order

When we say the terms are "in order", we are free to define what order that is! They could go forwards, backwards ... or they could alternate ... or any type of order we want!

Like a Set

A Sequence is like a Set, except:

• the terms are in order (with Sets the order does not matter)
• the same value can appear many times (only once in Sets)

Notation

Sequences also use the same notation as sets: list each element, separated by a comma, and then put curly brackets around the whole thing.

{3, 5, 7, ...}

That nearly worked ... but it is too low by 1 every time, so let us try changing it to:

                                    Test Rule: 2n+1

So instead of saying "starts at 3 and jumps 2 every time" we write this:

2n+1

Now we can calculate, for example, the 100th term:

2 × 100 + 1 = 201

Arithmetic Sequences

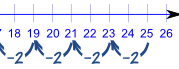
An Arithmetic Sequence is made by adding the same value each time.

Example:

1, 4, 7, 10, 13, 16, 19, 22, 25, ...

This sequence has a difference of 3 between each number.
The pattern is continued by adding 3 to the last number each time, like this:

Example:

3, 8, 13, 18, 23, 28, 33, 38, ...

This sequence has a difference of 5 between each number.
The pattern is continued by adding 5 to the last number each time, like this:

The value added each time is called the "common difference"

What is the common difference in this example?

19, 27, 35, 43, ...

Answer: The common difference is 8

The common difference could also be negative:

Example:

25, 23, 21, 19, 17, 15, ...

This common difference is −2
The pattern is continued by subtracting 2 each time, like this:

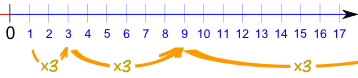
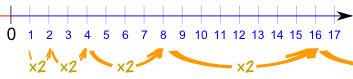
             Geometric Sequences

A Geometric Sequence is made by multiplying by the same value each time.

Example:

1, 3, 9, 27, 81, 243, ...

This sequence has a factor of 3 between each number.
The pattern is continued by multiplying by 3 each time, like this:

What we multiply by each time is called the "common ratio".

In the previous example the common ratio was 3:

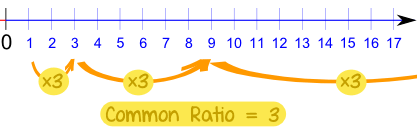
We can start with any number:

Example: Common Ratio of 3, But Starting at 2

2, 6, 18, 54, 162, 486, ...

This sequence also has a common ratio of 3, but it starts with 2.

Example:

1, 2, 4, 8, 16, 32, 64, 128, 256, ...

This sequence starts at 1 and has a common ratio of 2.
The pattern is continued by multiplying by 2 each time, like this:

The common ratio can be less than 1:

Example:

10, 5, 2.5, 1.25, 0.625, 0.3125, ...

This sequence starts at 10 and has a common ratio of 0.5 (a half).
The pattern is continued by multiplying by 0.5 each time.

But the common ratio can't be 0, as we would get a sequence like 1, 0, 0, 0, ...

References:

http://www.mathsisfun.com/algebra/sequences-series.html

https://www.mathsisfun.com/numberpatterns.html

https://www.youtube.com/watch?v=v63ho6h5VpQ