Mean, Median, Mode
Mean:
-- Also known as the average. The mean is found by adding up all of the given data and
dividing by the number of data entries.
dividing by the number of data entries.
Example:
- the grade 10 math class recently had a mathematics test and the grades were as
follows:
- the grade 10 math class recently had a mathematics test and the grades were as
follows:
78
66
82 464 / 6 = 77.3
89
75 Hence, 77.3 is the mean average of the class.
+ 74
464
66
82 464 / 6 = 77.3
89
75 Hence, 77.3 is the mean average of the class.
+ 74
464
Median:
-- The median is the middle number. First you arrange the numbers in order from lowest
to highest, then you find the middle number by crossing off the numbers until you reach the
middle.
to highest, then you find the middle number by crossing off the numbers until you reach the
middle.
Example:
- use the above data to find the median:
- use the above data to find the median:
66 74 75 78 82 89\
- as you can see we have two numbers, there is no middle number. What do we do?
It is simple; we take the two middle numbers and find the average, ( or mean ).
It is simple; we take the two middle numbers and find the average, ( or mean ).
75 + 78 = 153
153 / 2 = 76.5
Hence, the middle number is 76.5.
Mode:
-- this is the number that occurs most often.
Example:
- find the mode of the following data:
- find the mode of the following data:
78 56 68 92 84 76 74 56 68 66 78 72 66
65 53 61 62 78 84 61 90 87 77 62 88 81
65 53 61 62 78 84 61 90 87 77 62 88 81
The mode is 78.
https://www.youtube.com/watch?v=IV_m_uZOUgI
References:













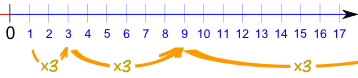
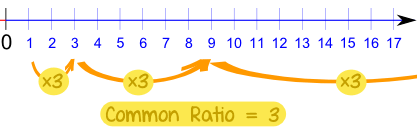

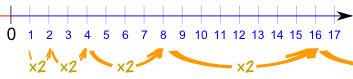
 and the common difference of successive members is d, then the nth term of the sequence (
and the common difference of successive members is d, then the nth term of the sequence ( ) is given by:
) is given by:


